What is symmetrical and asymmetric load?

In a normally functioning three-phase network, the linear voltages (voltages between each pair of phase conductors) are equal in magnitude and differ in phase by 120 degrees. Accordingly, the phase voltages (voltages between each phase conductor and the neutral conductor) are equal in magnitude and have similar phase differences.

As follows from the above, the phase angles between these voltages are equal to each other. This is called "Symmetric three-phase voltage system".

If you connect a symmetrical load to such a network, that is, a three-phase load at which the currents of each phase are equal in magnitude and phase, then such a load will create a symmetrical system of currents (with the same phase angle between them). This is possible provided that in all three phases of the load there are identical reactive and active resistances, that is, Za = Zb = Zc.

Therefore, the phase currents turn out to be equal in magnitude and in the phase angle between them under these conditions. Examples of symmetrical loads: a three-phase induction motor, three identical incandescent lamps - each in its own phase, a symmetrically loaded three-phase transformer, etc.

Consider a vector diagram of the currents of a symmetric three-phase load. It is easy to see here that the geometric sum of the vectors of the three phase currents vanishes. This means that with a symmetrical load, the current of the neutral conductor will be zero, and there is practically no need to use it.

If you connect an asymmetric load to this three-phase network with a symmetrical voltage system, that is, a load at which the complex load resistances in each phase are different (Za ≠ Zb ≠ Zc), then the load will create a system of currents that will differ in size and in direction (compared with the current diagram characteristic of a symmetrical load). The values ​​of these phase currents can be found according to Ohm's law.

And then the geometric sum of the currents will not turn to zero, which means that an alternating current will take place in the neutral conductor, so a neutral conductor is necessary in this case. Examples of asymmetric loads: incandescent lamps of different capacities in three phases, asymmetrically loaded three-phase transformer, loads with different power factors in three phases, etc.

The neutral wire in this case will ensure the conservation of phase voltage symmetry despite the fact that the load is asymmetrical. That is why a four-wire network allows the inclusion of single-phase consumers of different capacities and the nature of the impedance in different phases. The circuit of each loaded phase will be under the phase voltage of the generator, regardless of the difference in loads between the phases.

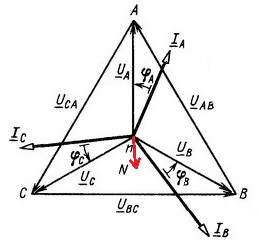
Here is a vector diagram of an asymmetric load. It is easy to see in the diagram that, due to the presence of a neutral wire, the current in it represents the geometric sum of the current vectors of each phase, while the phase voltages do not experience distortion, which would certainly have arisen if there had been no neutral wire with an asymmetric load.

If for some reason the neutral wire breaks during the supply of an unbalanced load, then there will be a sharp distortion of the voltages and currents of the three-phase network, which can lead to an accident.

The distortion will happen in this case because the three load circuits supplied by the three-phase source, together with the internal resistance of the source, form three circuits of different impedance, the voltage drop at each of which will be different and the voltage system of the three-phase network will therefore cease to be symmetrical.See more about this here:Causes and consequences of a zero wire break in the mains

Comments

[#1 Nikolay]

It is almost impossible to create the same phase load. According to experimental data, even in cable networks in Moscow and St. Petersburg, where the inputs to large residential buildings are, as a rule, three-phase, the phase loads differ by 20-25% or more, especially in houses with electric stoves.

Unbalanced loads cause a neutral bias and additional voltage deviations in individual phases of the network in different (positive and negative) directions. Bearing in mind that all voltage regulating means, as a rule, affect all three phases of the electric network, in order to ensure that voltage deviations from power receivers do not exceed acceptable limits, one has to focus on either correspondingly increased loads, or correspondingly reduced permissible voltage losses .

The magnitude of the asymmetry is detected by numerous and lengthy measurements at various points of the network, and after mathematical processing, correction factors are introduced into the calculation formulas, which then allow calculating the voltage loss, as for a network with a uniform phase load.

Yes, and with an asymmetrical load, phase voltage deviations consist of two components - deviations corresponding to the uniformly loaded network mode, and deviations determined by asymmetric loads.